Quantum Dots and their Application as Electron Spin Qubits

Overall, today I’ll be breaking my presentation into two major sections
So first I’ll be going over what Quantum Dots are, some of their core properties, and touch on a few methods for making quantum dots.
Then, to continue our showcase of different Quantum Computing Hardware
I’ll move on to how we can harness Quantum Dots to build what are known as Electron Spin Qubits.
So what an Electron Spin Qubit is, how they are made, and how they are used.
I want to point out that because Quantum Dots are such a rich topic there will be some aspects that I will have to gloss over,
So if you want more info, I will suggest some further reading



Alright, so what ARE quantum dots? Well, it’s a bit difficult to really illustrate without first talking about Dots in a somewhat abstract sense
The textbook definition is that a Quantum Dot is: “A system or structure fully confined in all three dimensions that exhibits discrete charge and electronic states”
So, you take a piece of material, confine it in 3D down to the nanoscale, I’m talking under 100nm
And if you do this, you’ll see some interesting characteristics will emerge. and there you go
According to this definition you have a Quantum Dot. Easy, A little bit of a broad/vague definition, but pretty straight forward yeah?
Well, what does that mean practically and how do we actually MAKE them, I’ll get to in a minute so keep that definition in mind
But first I need touch on the emergent properties and characteristics I mentioned that I think really what define Quantum Dots

Properties of Quantum Dots.
The emerging properties are what really are the distinguishing features of QDs
Mainly 1. These nanostructures are so tightly confined that they are said to be “0D” 2. They have bound, quantized energy states: Think back to the Harmonic Oscillator example 3. They have pretty well defined energy band structures (that we can manipulate, split, control charge movement) 4. Their electronic wavefunctions closely resemble those of actual atoms (Look at Kittel)
Because of these neat properties Quantum Dots have also been given the name “Artificial Atoms”

Alright so abstract discussion out of the way I can now go back to how we actually make Quantum Dots
So there are several different ways of making structures and systems that exhibit the properties that we talked about before
We just need to find a way to confine a system in 3D
That’s why the definition can seem somewhat broad and vague. There are multiple ways of getting to the same properties.
I’d like to highlight a 4 of ways to make Quantum Dot structures
One way of making a dot is Single Molecule traps, not unlike what we talked about earlier with our first guest speakers - where we trap whole molecules in between electrodes and manipulate them there
Another way we can go about making a QD is by synthesizing metallic particles with chemistry - Actually, this is kind of cool because of how quick it is: check out videos on Youtube
A third way which is fairly popular in the world of silicon photonics is Vertical Semiconductor QDs - Build up layers of material, then etch down these column structures and you get a confined dot
Finally, what will be the focus of the remainder of my talk: Lateral Semiconductor Dots - Voltage Corals - Where we use processes common in Semiconductor fab processes to lay out the dots in a planar arrangement



Alright so now, I’d like to switch gears a little bit and begin talking about Qubits and Quantum Computers
Just so that we have a bit of an understanding of what we’re working toward
In the late 90s, early 2000s, David DiVincenzo proposed a set of criteria necessary for building a quantum computer. Aptly named the DiVincenzo Criteria
And while these criteria were initially meant to characterize the computer as a whole,
they actually work well to describe the criteria necessary for the qubits that make up that computer
So for a good Qubit, we want to be able to: - Initialize: Get a Qubit into a known and stable state - Manipulate: Or act on it with a set of gates - Readout: After some manipulations, we want to be able to determine what state we are in - Keep them for a long time: Or have keeping them isolated from the environment as much as possible to mitigate decoherence - Scale: Have multiple qubits available to work with
So that’s what we want to see with our Qubits
Now for the rest of my time, I’ll be going over how we can use Lateral semiconductor dots to make what are called Electron Spin Qubits
And go over in a little more detail how we can meet the criteria above

Electron Spin Qubits are Qubits that use the spin orientation of an electron (Spin Up and Spin Down) as the basis for the qubit
Here we have our good friend the Bloch Sphere to illustrate what I’m talking about

And here I’ll go through a little demonstration of how we trap a single electron to make our Qubit
The way that we make them with quantum dots is that we start with a sea of electrons
Then we apply a voltage via electrodes, so that we form a little electron puddle corralled by the electrodes
Once we have a well-defined dot, we pump out the electrons one by one until we only have one electron left.
Now have a well defined Quantum Dot with a single electron and a single controllable spin
which means we have a well defined Electron Spin Qubit

So we have our trapped electron, now we want to actually do something with it.
First, like our DiVincenzo Criteria says, we have to initialize it, or in other words, we want to put it in a known stable state
How we do this is to apply a strong magnetic field at low temp so that there is a distinct Energy difference between the Up and Down states of the electron
Then we want to apply a voltage pulse so that we bring just one energy level below the Fermi Energy.
We are making it so that we can only trap electrons in this particular state
So we have initialized our Qubit in the Spin Up state

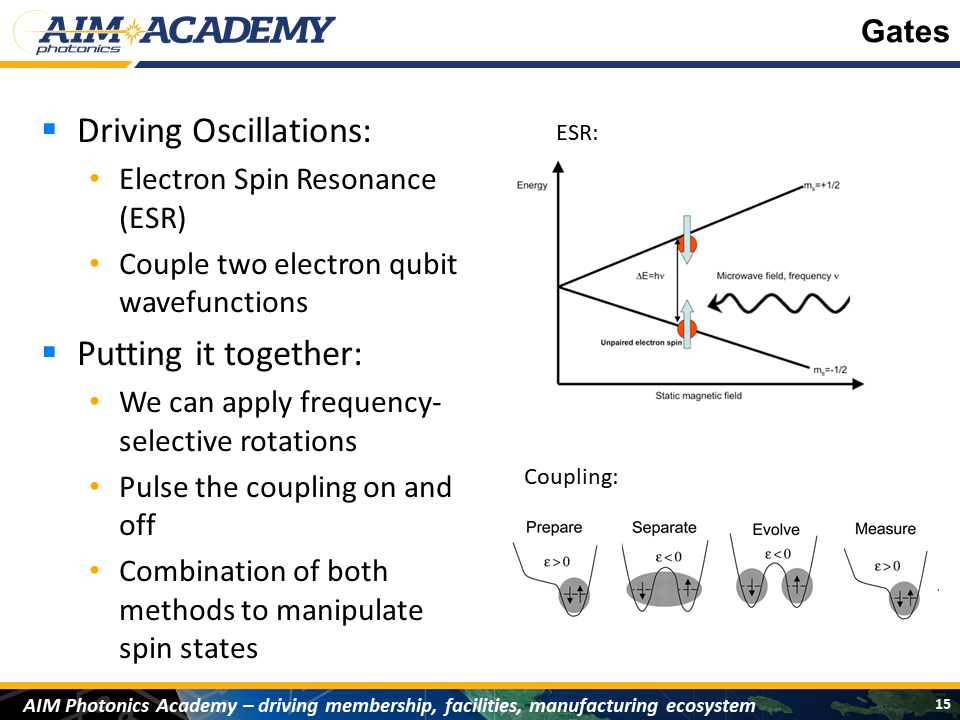
Now we want to apply some gates to the qubit. Well first, we make sure the qubit is trapped so that it cant escape (so both up and down are below the Fermi Level):
Then we can do this in one of two ways: - Electron Spin Resonance (ESR): Using an oscillating magnetic or electric fields to drive transitions from spin up to spin down - Or we can take a more indirect approach by letting the interactions between electrons themselves act as the manipulation: Couple two electron qubit wavefunctions
Now, final state of the electrons depend on each other

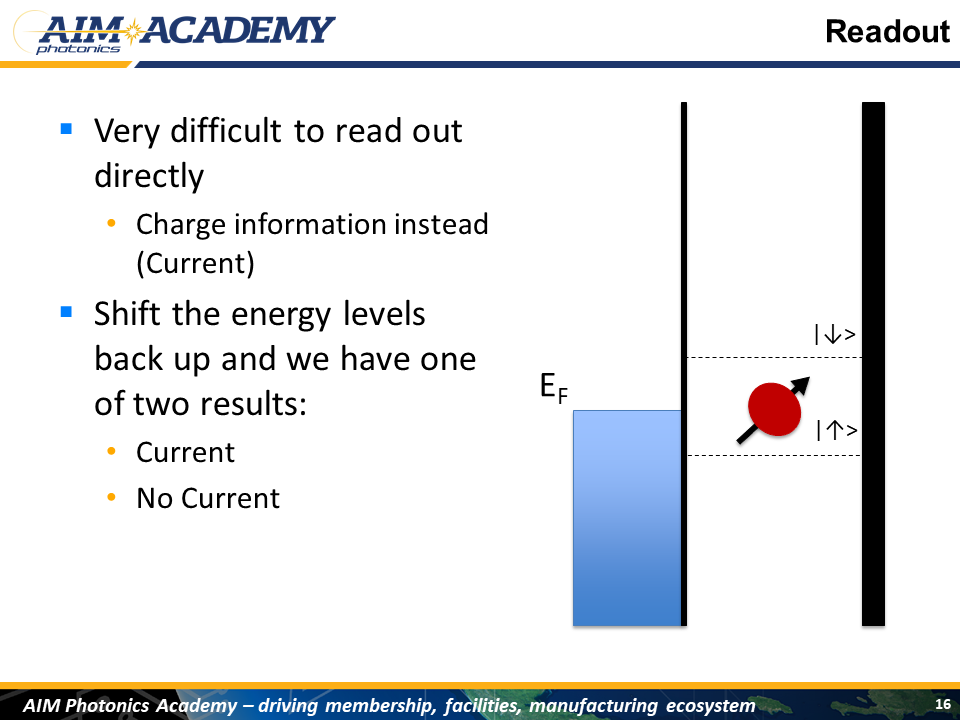
After applying the gates, we’ll want to readout the final state of our qubit
Now this is kind of tricky because we can’t actually directly measure the spin of an electron
Well, we can, but it's really impractical, especially with this application.
So there’s this clever way of reading out where we can measure current to determine the state of the qubit.
Read the current coming out of the Qubit
So the premise is that we shift our energy states back up to where they were before and depending on which state the qubit is in, we will either measure a spike in current, or we wont measure anything
Let’s go through this:

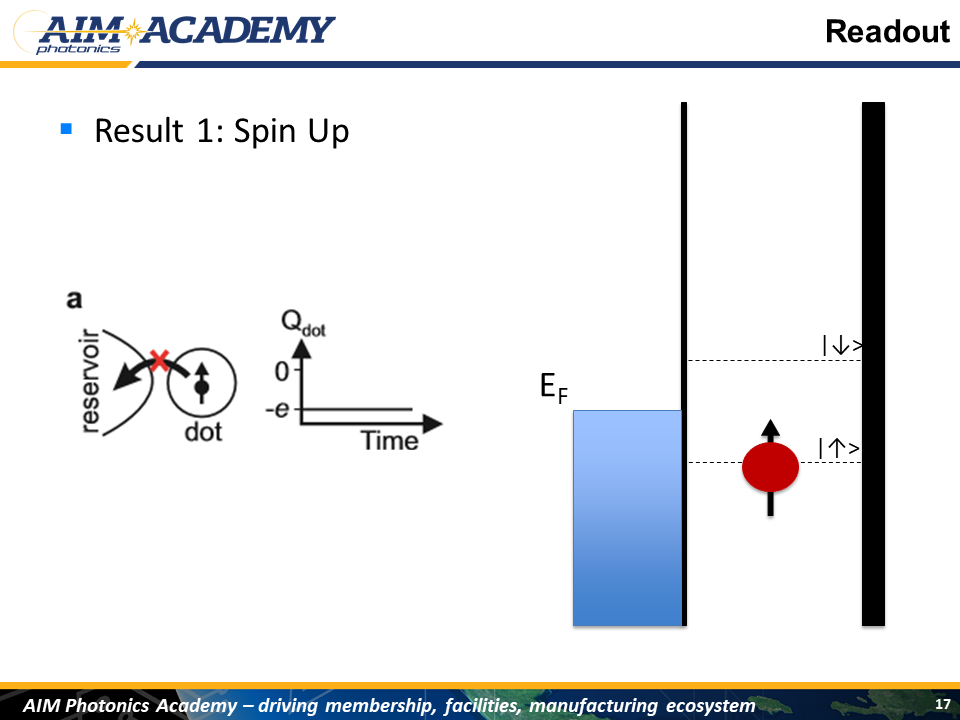
First Result:
After we’ve done some manipulation we basically do the reverse of initialization
Spin Up:
We push the levels back up, but since the electron is in the spin down state, it is below the Fermi level and will not escape from the trap

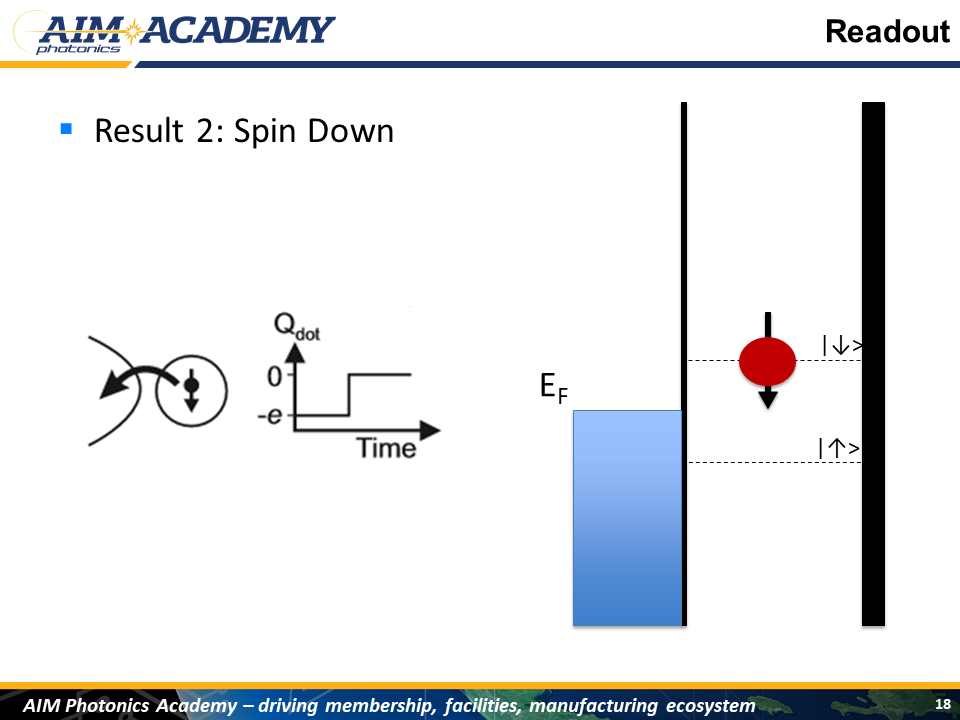
Second Result:
After we’ve done some manipulation we basically do the reverse of initialization
Spin Down:
We push the levels back up, and since the electron is in the spin up state, it is above the Fermi level and will escape back into the sea of electrons
Comment from Jiji:
Fermi level E_F should be between up state and down state energy. Such that the qubit energy is below Fermi level when it is in the up state; above Fermi level when it is in the up state.

One last note on the final part of the DiVincenzo Criteria:
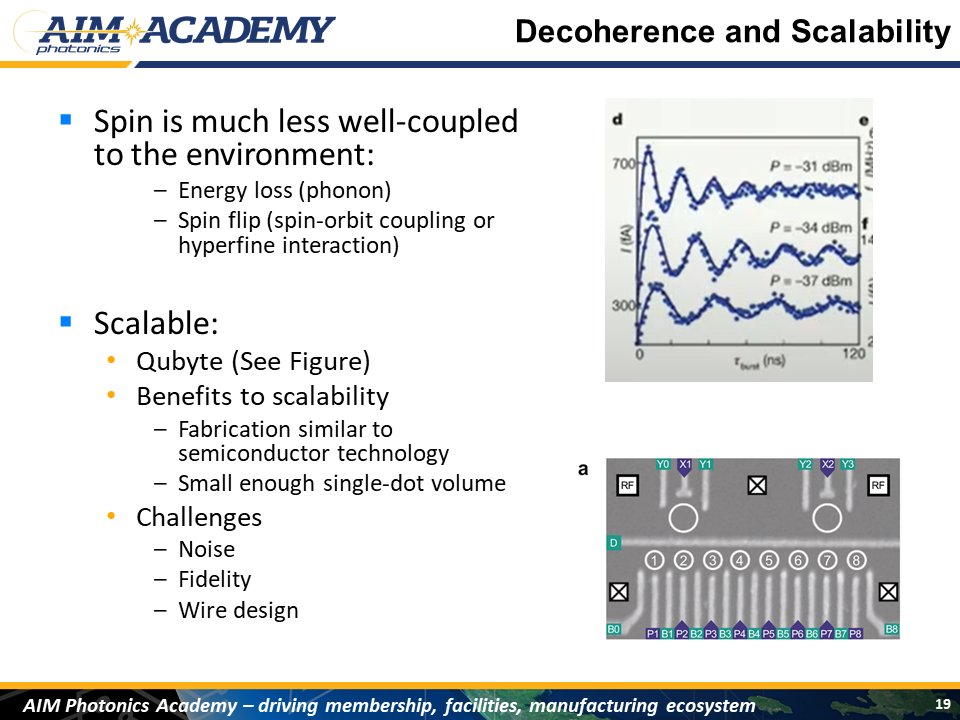
I want to point out that Spin Qubits are nice because of how much effort it takes to decohere - You need two coupling mechanisms in order for the qubit to lose energy
Also, they are very scalable. - Example: The Qubyte (8 Qubits)
Comment from Jiji:
Here are some comments about scalability of quantum dot. Silicon QD is based on solid state physics and the fabrication can be fit into flourishing semiconductor technology to some degree. Also, a QD qubit is essentially an electron confined in a potential well, so the volume of single dot would be small enough for scaling. These are pros about scalable QD qubit.
However, comparing to superconducting qubit, QD qubit is more noisy. Since superconducting qubit use relatively macroscopic phenomena (Josephson junction); while QD is only an microscopic electron. It’s hard to construct multi qubit QD device and maintain the fidelity at the same time.
There is a challenge shared for any kind of qubit when talking about scalability: wire design. For QD system, we need different on resonance frequency for each qubit, and each of the frequencies should not be to close in order to avoid crosstalk error. Additionally, we need localized AC magnetic field to control qubits individually. How to achieve frequency split and localized control without messy wire design is also a huge challenge.



Alright, and that’s the end!
Thanks for listening, if you are interested in the topic some more, I suggest looking up the resources here.
Thank you